Bond convexity is a measure of the curvature in the relationship between the bond prices and bond yields. In other words, the degree of sensitivity of a bond to interest rate fluctuations – not just in a straight line, but along a curve. The term is a second-order derivative of the price equation and is relevant in the context of bond risk management strategy.
Bond Convexity
Bond convexity is a crucial concept that helps investors to understand how bond prices respond to changing interest rates environments than the duration estimates. By understanding convexity, investors can compare bonds more effectively and understand risk management, especially in volatile market conditions.

Explore Bonds by Category
High Yield

ICRA BBB
You Invest
₹9,949
Returns (YTM)
13.25%
You Get
₹11,493
Today
15 months
Invest in Tencent Backed, Digitally-Driven NBFC Managing an AUM of 1,700+ Cr
You Invest
₹9,949
Returns (YTM)
13.25%
You Get
₹11,493
Today
15 months
Invest in Tencent Backed, Digitally-Driven NBFC Managing an AUM of 1,700+ Cr
ICRA BBB
ACUITE BBB+
You Invest
₹9,800
Returns (YTM)
13.25%
You Get
₹12,680
Today
34 months
Listed NBFC, 670+ Cr AUM with 100% Secured Lending
You Invest
₹9,800
Returns (YTM)
13.25%
You Get
₹12,680
Today
34 months
Listed NBFC, 670+ Cr AUM with 100% Secured Lending
ACUITE BBB+

CARE BBB+
You Invest
₹1,01,274
Returns (YTM)
12.75%
You Get
₹1,17,652
Today
28 months
Listed NBFC backed by Kedaara Capital with 47% Capital Adequacy Ratio
You Invest
₹1,01,274
Returns (YTM)
12.75%
You Get
₹1,17,652
Today
28 months
Listed NBFC backed by Kedaara Capital with 47% Capital Adequacy Ratio
CARE BBB+
What is Bond Convexity
How to Buy Bonds through Paisabazaar?
Get up to 13.25% from bonds in 5 simple steps
Step 1: Login to your Paisabazaar account
Step 2: Select the Bonds
Step 3: Complete the KYC process
Step 4: Enter bank details
Step 5: Link your demat account
Understanding Why Bond Convexity Matters
To understand the concept of bond convexity, we need to understand the ‘duration’, which is considered the first order derivative of the bond price equation. Duration measures how sensitive your bond is to changes in interest rates. It assumes a linear relationship between bond yield changes and changes in price. But, this relationship isn't actually linear when interest rates change by large shifts—it's curved. Convexity corrects this error and provides a more accurate prediction.
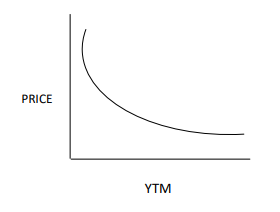
Example
To understand convexity and duration better, let me compare it to driving a car. The speed of the car is referred to as the duration. While the driver is speeding up or slowing down (i.e., the rate of change), the car is called convexity. In relation to the bond market, the higher the convexity, the more drastic the change would be in the price given a move in interest rates.
Formula for Calculating Bond Convexity
Convexity = (1 / P) * Σ [(Ct * (t² + t)) / (1 + y)^(t+2)]
Where:
‘P’ is the current price of the bond
‘Ct’ is the cash flow at time ‘t’
‘y’ is the yield to maturity
‘t’ is the time period in years
Let’s take an example
ABC Ltd. has issued bonds having a face value of Rs 1,000 with a coupon rate @ 10% p.a. The maturity period of the bond is 3 years. The yield to maturity is 10% and the prevailing current bond price is Rs 1,000.
Let’s calculate convexity:-
First, we need to identify cash flows, i.e., ‘Ct’
| Year | Cash Flow |
|---|---|
| 1 | 100 |
| 2 | 100 |
| 3 | 1,100 (1,000 +100) |
Now, applying the bond convexity formula:-
For the year 1
Cash Flow (Ct): 100
Time period (t): 1
Yield to maturity (y) = 10% = 0.10
Convexity: [(100 * (1² + 1)) / (1 + 0.10)^(1+2)] = 150.26
For the year 2
Cash Flow (Ct): 100
Time period (t): 2
Yield to maturity (y) = 10% = 0.10
Convexity: [(100 * (2² + 2)) / (1 + 0.10)^(2+2)] = 409.77
For the year 3
Cash Flow (Ct): 1100
Time period (t): 3
Yield to maturity (y) = 10% = 0.10
Convexity: [(1100 * (3² + 3)) / (1 + 0.10)^(3+2)] = 8197.45
Summing the values of convexity
150.26+ 409.77+8197.45 = 8757.48
Dividing by bond’s price = 8757.48/1000 = 8.757 or 8.76
The value 8.76 means the bond has positive convexity.
People also search for
Difference between Convexity & Duration
| Differentiation Factor | Convexity | Duration |
|---|---|---|
| Relationship | Measures the curvature of the price-yield relationship | Assumes linear relationship - straight line |
| Measures | Change in price sensitivity | Price sensitivity |
| Calculus Order | Second derivative of price-yield function | First derivative of price-yield function |
| Accuracy Level | Accurate for large interest rate movements | Accurate for small interest rate changes |
| Impact When Interest Rates Fall | Predicts higher price appreciation than the duration predicts | Predicts price increase using a straight-line estimate |
| Impact When Interest Rates Rise | Shows a smaller price decline than the duration predicts | Predicts price decline using a linear estimate |
Positive Convexity & Negative Convexity
Positive convexity refers to a bond's price rising faster when bond yields fall and falls slower when yields rise. This benefits investors with more upside than downside, which is seen in most regular corporate bonds, government bonds, or plain vanilla bonds. Negative convexity is seen in callable bonds, as such bonds have a ceiling on their price. When interest rates fall, bonds are usually called, i.e., limiting upside for investors. And, when interest rates rise, the bond won’t be called, i.e., full downside for investors. This creates a negative convexity, which hurts investors by limiting upside and worsening losses.
Bonds Having Higher Convexity
Zero-coupon bonds, non-callable corporate bonds and long-term government bonds have higher convexity. Zero coupon bonds have higher convexity because their entire cash flow is received at the maturity period. This makes the present value of the bond extremely sensitive to interest rate changes in the market, which results in a pronounced curve in the price-yield relationship. The price swings are high for bonds with longer maturity periods.
Is Higher Bond Convexity Good?
Higher positive convexity is considered good for investors because it offers greater upside potential and downside protection. Upside potential here refers to the faster increase in the bond's price when interest rates fall and downside protection means the bond's price falls less when interest rates rise. However, such bonds often come with lower yields and higher prices. Therefore, investors should balance high bond convexity benefits with their investment objectives and the return potential. Ignoring convexity in the portfolio can lead to underestimating the bond risk during an environment of sharp rate movements.
How to Buy Bonds through Paisabazaar?
Get up to 13.25% from bonds in 5 simple steps
Step 1: Login to your Paisabazaar account
Step 2: Select the Bonds
Step 3: Complete the KYC process
Step 4: Enter bank details
Step 5: Link your demat account
FAQs
Bonds Articles
View All ArticlesCheck Top Bond Offers with Assured Returns of up to 13.25%
Paisabazaar is a loan aggregator and is authorized to provide services on behalf of its partners
*Applicable for selected customers











